La Regola Del 72 Negli Investimenti

Quando la nostra banca ci offre un investimento del 4% netto annuo (5,48% lordo), come possiamo capire se tale investimento sarà conveniente per noi? Innanzitutto, dobbiamo avere ben chiaro in mente il nostro obiettivo: se è quello di raddoppiare il capitale in 9 anni, il 4% netto offerto dalla Banca non è l’investimento ideale. Ecco che allora in nostro soccorso arriva la regola del 72. La “regola del 72” è una pratica comune utilizzata nella finanza per stimare rapidamente il numero di anni necessari per raddoppiare una somma di capitale, con un dato tasso d’interesse annuale, oppure per stimare il tasso d’interesse annuale che serve per raddoppiare una somma di denaro in un dato numero di anni.

In sostanza, tale regola afferma che “il tasso di interesse moltiplicato il numero degli anni necessari a raddoppiare la sorte capitale è pari a circa 72“. Vale a dire che dividendo per 72 l’annuale tasso di rendimento di un investimento, gli investitori potranno ottenere una stima approssimativa di quanti anni ci vorranno all’investimento iniziale per raddoppiare di valore. Facciamo un esempio pratico. Poniamo R * T = 72, dove R = tasso di crescita (per esempio, il tasso d’interesse), T = tempo di raddoppio (per esempio, il tempo necessario a raddoppiare un ammontare di denaro). Ipotizziamo di voler conoscere quanto sia necessario per raddoppiare € 100 al tasso d’interesse annuale del 5%? Sapendo che R = 5, otteniamo 5 * T = 72. Nell’esempio dato, dovremo dividere entrambi i lati per R = 5, per ottenere T = 72/5 = 14,4. Quindi ci vogliono 14,4 anni per raddoppiare il nostro investimento di 100 Euro ad un tasso d’interesse annuo del 5%. Quando si tratta di bassi tassi di rendimento, la Regola del 72 è abbastanza precisa. Il grafico sottostante mette a confronto i numeri dati dalla regola del 72 e il numero effettivo di anni necessari ad un investimento per raddoppiare.

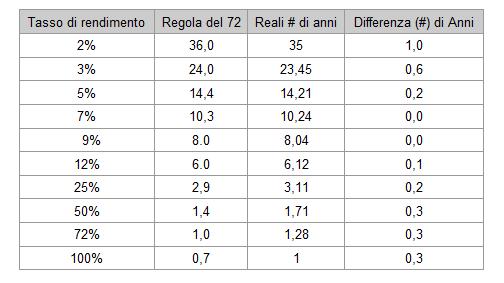
Ad ogni modo, anche se riesce a dare una stima approssimativa abbastanza veloce, la regola del 72 è meno precisa quando ci troviamo in presenza di alti tassi di rendimento. Quindi, in tali situazioni, sarebbe opportuno calcolare il numero preciso di anni in modo “algebrico” mediante il valore futuro della formula.